Für Interessierte gibt es hier einen technischen Überblick zum Aufbau und der Funktion eines FMCW Radar Altimeter.
Frequenz-Arbeitsbereich eines FMCW Radar Altimeter
Ein FMCW Radar Altimeter arbeitet in einem hochfrequenten Frequenzbereich von mehreren Gigahertz (GHz), auf dieser Seite werden zwei Frequenzbereiche vorgestellt (4.3 GHz Flugzeug Radar Altimeter und 24 GHz Universal Radar Altimeter).
Als Beispiel:
1 GHz entspricht 1e9 Hz = 1 000 000 000 Hz, also einer Milliarde Schwingungen pro Sekunde
Zum Vergleich:
Der Radio-UKW-Bereich befindet sich in einem Frequenzbereich von ca. 100 MHz, das Satellitenfernsehen bei ca. 12 GHz.
Dieses hochfrequente Signal wird über eine Antenne als elektromagnetische Welle in den Raum abgestrahlt.
Frequenz-Zeit-Diagramm bei FMCW
Abbildung 1 zeigt das Grundprinzip eines FMCW Radar Altimeter. FMCW steht für „frequency modulated continuous wave radar“. Es illustriert eine kontinuierliche lineare Änderung der Frequenz über die Zeit (Frequenzmodulation, hier in Form eines Dreieckssignals). Das rote Signal stellt das Sendesignal dar („S“), in blau das Empfangssignal („E“). Δt ist der zeitliche Versatz zwischen Sende- und Empfangssignal aufgrund der Signallaufzeit, Δf ist die daraus resultierende Differenzfrequenz zwischen den beiden Signalen zu einem bestimmten Zeitpunkt.
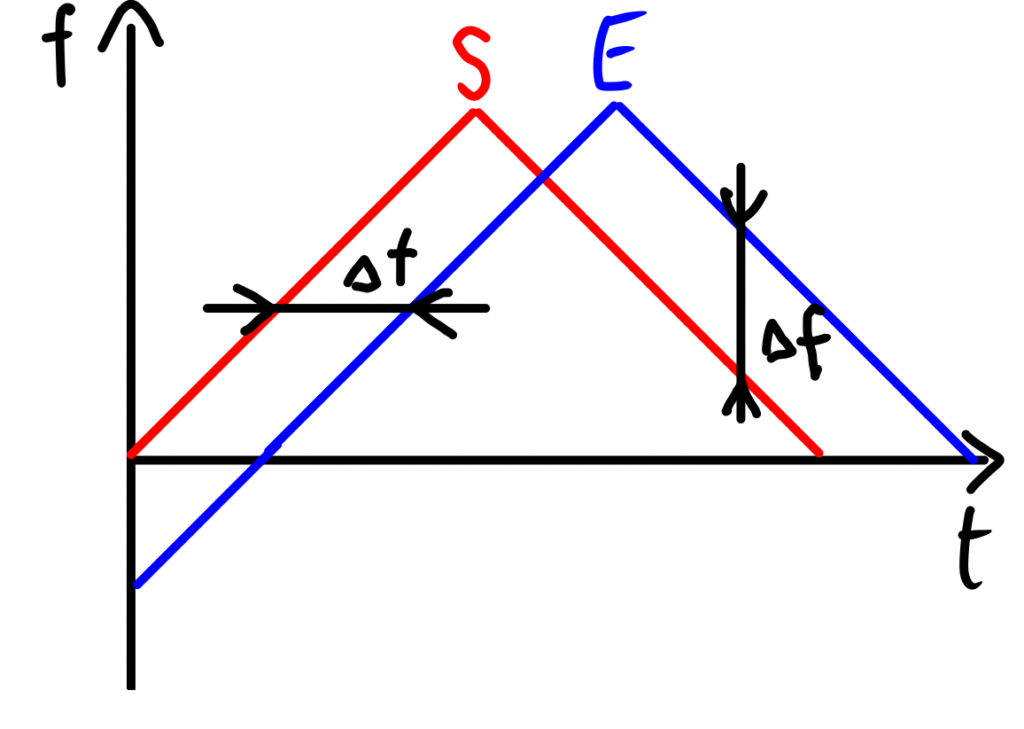
Zeitlicher Signalverlauf bei FMCW
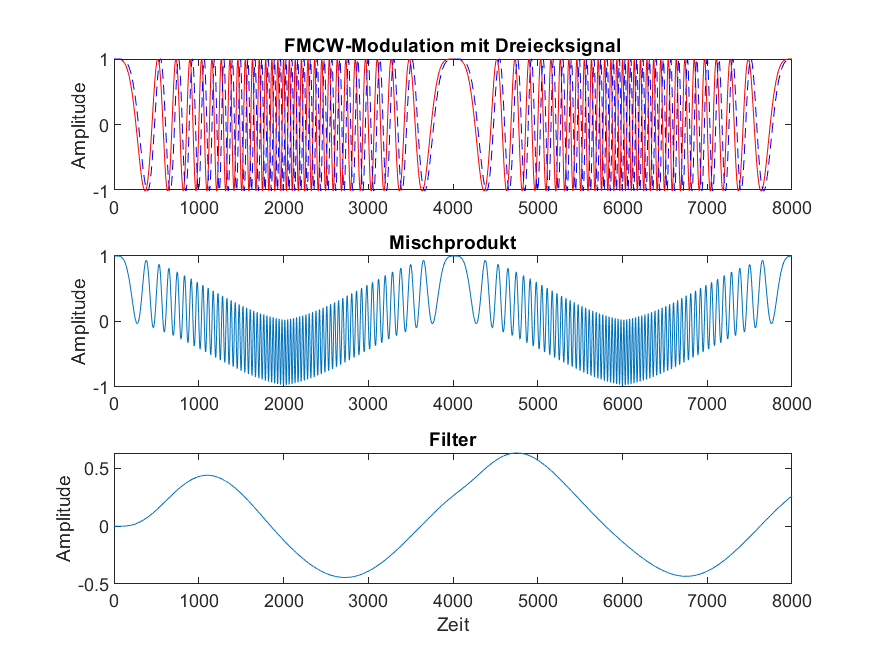
Abbildung 2 zeigt drei Plots im Zeitbereich. Der oberste Plot stellt das dreieckförmig modulierte Signal des Senders (ROT) dar, das Empfangssignal ist verzögert um den zurückgelegten Weg bzw. der entsprechenden Zeitdauer (BLAU strichliert). Die beiden Signale werden miteinander gemischt (vereinfacht gesagt multipliziert) und als Ergebnis erhält man ein Mischprodukt (mittlerer Plot), das sind prinzipiell Summen- und Differenzfrequenzen zwischen gesendetem und empfangenen Signal.
Anschließend wird das Mischsignal elektronisch gefiltert, insbesondere wird damit das hochfrequente Summensignal entfernt, übrig bleibt die Differenzfrequenz (gefiltertes Mischsignal, unterster Plot).
Diese Differenzfrequenz bildet ein Maß für die Entfernung bzw. Höhe.
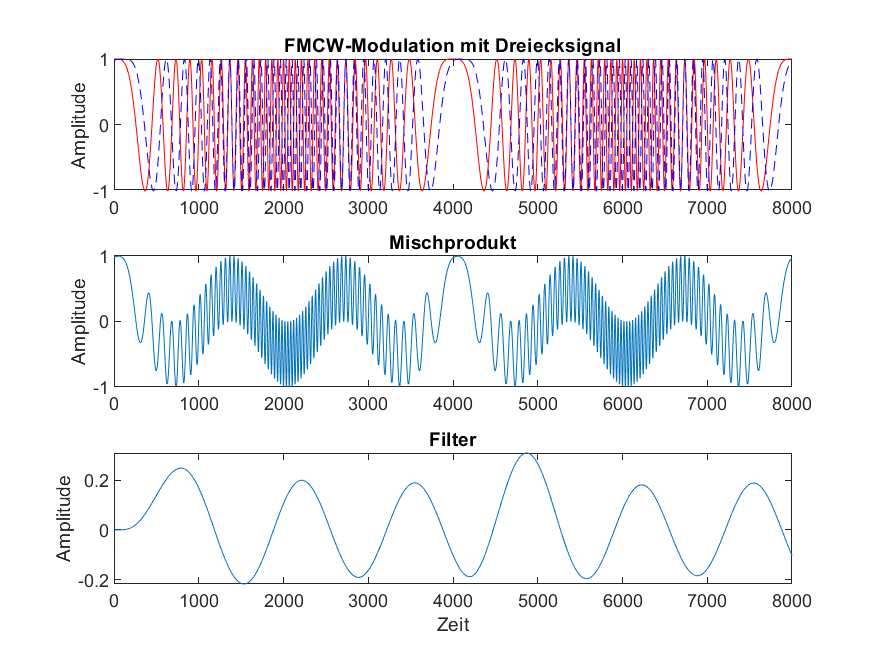
Gegenüber Abbildung 2 ist in Abbildung 3 ein weiteres Beispiel angeführt, wo das Flugobjekt etwas höher fliegt – die Differenzfrequenz steigt!
Mathematisch lässt sich die Höhe einfach beschreiben als Lichtgeschwindigkeit (c) multipliziert mit der halben Zeitdifferenz (Δt). Die Halbierung rührt daher, da das Signal zum Boden eine Strecke und das reflektierte Signal zurück eine weitere, also in Summe doppelte Strecke zurücklegt.
df/dt beschreibt die differentielle Frequenzänderung über die Zeit. Nachdem es sich um eine lineare Frequenzänderung handelt (zumindest theoretisch, siehe Abbildung 1), entspricht das der Steigung des Dreiecksignals im Frequenz-Zeit-Diagramm. Das Verhältnis Δf/Δt gibt dieselbe Steigung an.
Somit sind auf der rechten Seite der Gleichung bis auf die zu messende Differenzfrequenz Δf alle Parameter bekannt.
(1) ![]()
(2) 
(3) 
Signalverarbeitung eines FMCW Radar Altimeter
Anschließend wird das Signal elektronisch gefiltert und verstärkt um danach mittels eines Analog-Digital-Wandlers digitalisiert und z.B. mit einem Mikrocontroller (ein programmierbarer integrierter Schaltkreis bestehend aus CPU, Speicher und Peripherie; also ein kleiner Computer) weiterverarbeitet zu werden.
Im Computer werden verschiedene Methoden der digitalen Signalverarbeitung angewendet, insbesondere wird das Signal meistens im Frequenzbereich analysiert. Zum Schluss gibt der implementierte Algorithmus die daraus abgeleitete Höhe aus, die über eine Schnittstelle (ARINC 429, RS485, RS232) digital oder manchmal auch analog zur Verfügung gestellt wird.
Dopplerfrequenz bei Radialgeschwindigkeit
Wenn das Flugobjekt steigt oder sinkt, ändert sich auch die Differenzfrequenz zusätzlich um die Dopplerfrequenz. Die Steig- oder Sink-rate lässt sich neben der Höhenmessung durch Kombination von an- und absteigender Frequenzrampe bei dreieckförmiger Modulation berechnen.
Praktisch müssen für die zuverlässige Funktion bzw. Robustheit eines FMCW Radar Altimeter noch einige weitere Faktoren berücksichtigt werden, die hier nicht angeführt sind da sie zu sehr ins technische Detail gehen würden.
